3.7 - The Wandering Ant on a Square Grid

HandsOn Activities:

12. Random Walk in 2-Dimensions

SimuLabs:

9. The Deer Program and Population Dynamics

Suppose that the ant is not forced to step just along a line, but can move in four mutually perpendicular directions when walking away from the lamp post. This type of movement is called a 2-dimensional random walk.

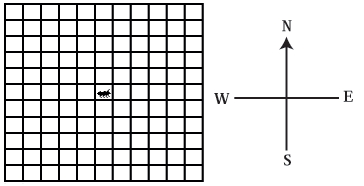
For example, an ant is standing in the center of a 11 by 11 grid, as shown in Figure . Each grid square is the size of one step. The ant can move one step at a time in one of four directions: north, south, east, or west. The ant cannot move diagonally or take more than one step at a time. If the ant walks off the edge of the grid, it cannot return.

Q3.38: Where do you think the ant will most likely be after 100 steps? Will it still be on the grid?

Q3.39: Let's say we place 1000 ants on the center square of the grid. If each ant moves independently using the same rules as above, how do you think the ants will be distributed on the grid after each ant has taken 10 steps? 100 steps? 1000 steps?

Q3.40: Is there a relationship between random walks and coin flipping? If so, what is this relationship?

  Previous: 3.6 - Proving Average Squared Difference