

Next: About this document
Up: Simulations with the
Previous: Solvation of a
Background :
A simulation is only a model.
For this reason, whenever looking at the microscopic
properties of water, one should question whether or not
the investigated system size is large enough.
In statistics we learn that statistical accuracy increases with the number
of particles in the sample.
For example, if we investigate a 96 particle system, we are
looking at 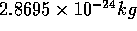 of water.
In contrast, even a milliliter of water at room temperature has a much
greater mass:
of water.
In contrast, even a milliliter of water at room temperature has a much
greater mass:  , and a corresponding larger number of particles.
A good method of determining the accuracy of the
simulation is to calculate the deviations of fluctuating quantities.
For example, given any equilibrated system size, the potential energy should
fluctuate by a maximum of about
, and a corresponding larger number of particles.
A good method of determining the accuracy of the
simulation is to calculate the deviations of fluctuating quantities.
For example, given any equilibrated system size, the potential energy should
fluctuate by a maximum of about 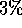 . Other properties that can be studied,
depending on the simulation setup (NVT or NPT ensemble), are the pressure
p and the density
. Other properties that can be studied,
depending on the simulation setup (NVT or NPT ensemble), are the pressure
p and the density  . You will observe that the pressure deviation is very large
in comparison to the smaller deviations of the density.
This arises from the fact that water has a very small compressibility factor
(
. You will observe that the pressure deviation is very large
in comparison to the smaller deviations of the density.
This arises from the fact that water has a very small compressibility factor
( ).
The fluctuation of the volume (and thus of the density) and of the pressure are
dependent on the compressibility, but in different ways.
The result is that the deviations of the volume are diminished
by small compressibility
whereas the deviations of the pressure are enhanced.
).
The fluctuation of the volume (and thus of the density) and of the pressure are
dependent on the compressibility, but in different ways.
The result is that the deviations of the volume are diminished
by small compressibility
whereas the deviations of the pressure are enhanced.
Think of a ball bearing bouncing on a block of steel. The steel
has a very small compressibility factor, so the
ball bearing experiences large forces (``pressure'') at every
bounce, while the density of the steel block remains nearly constant.
This image corresponds to the large fluctuations in pressure and low
fluctuations in density in a small sample of water.
A side effect has to be kept in mind when
simulating an ion in water. The theoretical assumption is that the ion is in
infinite dilution (meaning an extremely low concentration.)
This assumption implies that inter--ionic
interactions (interactions between one ion and a neighboring ion)
do not have to be considered.
However we use periodic boundary conditions
in our simulation. Therefore in a system that is too small, the ion will
interact with its own image.
As far as the computer simulation is
concerned, all the other images of ions are ``really there'',
with consequences for interaction energy that cannot be ignored.
If the central box size is large enough (system size sufficiently great),
the interaction energy
will be close to zero and its contribution can be neglected.
To test this, one should compare the simulated box size with a normal plot
of the Coulomb potential.
If the potential is not close to zero at a distance equal to half
the simulated box size, then
the box size should be increased to embrace a larger system
(half the box size because of the periodic
boundary conditions - this is the maximum distance between two particles
-- see also Fig. 4.10.1.)
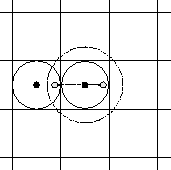
Fig. 4.10.1
The maximum distance between two particles must be less than half
the box length
(represented by the solid line circle around the center particle.)
The particle interacts with one other particle within this sphere. If we apply
periodic boundary conditions, then all images behave accordingly.
If the distance is increased to a radius larger than half the box length (represented
by the dashed circle around the center particle), then we would calculate the
interaction with a particle and its image. The image however is not a real
particle. It is a mere artifact of the periodic boundary conditions.
A similar difficulty arises for noble gases.
The potential used to calculate the interaction between water molecules
and a noble gas is the Lennard--Jones potential.
We decrease the ``false'' interaction of a particle with its own image by
increasing the size of the simulation box. To do this we keep the density of particles
the same but increase the number of particles in the box, thus pushing out
its boundaries. (Density of particles is defined as the number of particles
per unit volume.)
More particles means a greater computational load on the computer,
which is why the Wasser program requires fast computers!
The box length  can be determined by calculation
from the density and the number of particles,
can be determined by calculation
from the density and the number of particles,

where 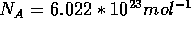 is the Avogadro constant,
is the Avogadro constant,
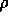 is the density in
is the density in 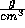 ,
N is the number of particles in the system and M
is the molar mass of water. Please keep the units in mind - the box length is
usually given in units of nm (
,
N is the number of particles in the system and M
is the molar mass of water. Please keep the units in mind - the box length is
usually given in units of nm (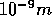 ).
).
Questions :
- Why do molecules in water have such a high average kinetic energy?
- Suppose we want to increase the size of our system. Is it
sufficient to simply reduce the density of our existing system?


Next: About this document
Up: Simulations with the
Previous: Solvation of a
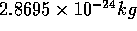 of water.
In contrast, even a milliliter of water at room temperature has a much
greater mass:
of water.
In contrast, even a milliliter of water at room temperature has a much
greater mass:  , and a corresponding larger number of particles.
A good method of determining the accuracy of the
simulation is to calculate the deviations of fluctuating quantities.
For example, given any equilibrated system size, the potential energy should
fluctuate by a maximum of about
, and a corresponding larger number of particles.
A good method of determining the accuracy of the
simulation is to calculate the deviations of fluctuating quantities.
For example, given any equilibrated system size, the potential energy should
fluctuate by a maximum of about 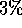 . Other properties that can be studied,
depending on the simulation setup (NVT or NPT ensemble), are the pressure
p and the density
. Other properties that can be studied,
depending on the simulation setup (NVT or NPT ensemble), are the pressure
p and the density  . You will observe that the pressure deviation is very large
in comparison to the smaller deviations of the density.
This arises from the fact that water has a very small compressibility factor
(
. You will observe that the pressure deviation is very large
in comparison to the smaller deviations of the density.
This arises from the fact that water has a very small compressibility factor
( ).
The fluctuation of the volume (and thus of the density) and of the pressure are
dependent on the compressibility, but in different ways.
The result is that the deviations of the volume are diminished
by small compressibility
whereas the deviations of the pressure are enhanced.
).
The fluctuation of the volume (and thus of the density) and of the pressure are
dependent on the compressibility, but in different ways.
The result is that the deviations of the volume are diminished
by small compressibility
whereas the deviations of the pressure are enhanced.

 can be determined by calculation
from the density and the number of particles,
can be determined by calculation
from the density and the number of particles,

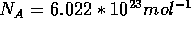 is the Avogadro constant,
is the Avogadro constant,
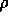 is the density in
is the density in 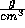 ,
N is the number of particles in the system and M
is the molar mass of water. Please keep the units in mind - the box length is
usually given in units of nm (
,
N is the number of particles in the system and M
is the molar mass of water. Please keep the units in mind - the box length is
usually given in units of nm (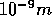 ).
).